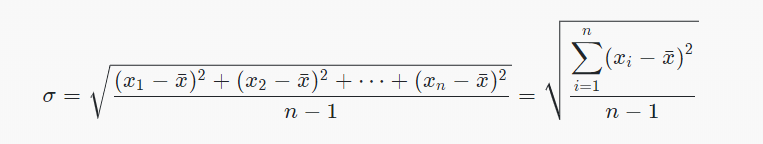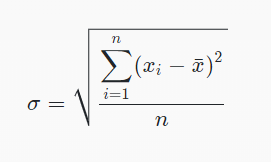Calcula fácilmente la desviación típica muestral y poblacional y averigua cuál es la diferencia entre cada uno de estos conceptos.
Calculadora de desviación estandar
Hacemos referencia a la desviación estándar o también denominada típica cuando hablamos de un valor que cuantifica la dispersión de un conjunto de números. La calculadora estadística de la desviación estándar puede asociarse a un valor bajo a o un valor alto. Un valor bajo de la desviación típica indica que los números del conjunto están relativamente concentrados alrededor de la media. Por el contrario, un valor alto de la desviación estándar representa una mayor extensión del rango de valores. Puedes encontrar esta dato estadístico representado con la letra griega sigma (σ). 
Cómo funciona la Calculadora de Desviación Estándar
El funcionamiento de esta calculadora de matemáticas es muy sencillo. Basta con escribir los diferentes números (tanto con valores positivos como negativos) en el espacio superior de la calculadora. Inmediatamente la herramienta ofrecerá su resultado.
Hasta finalmente obtener el dato que estás buscando: la desviación típica.
Cómo calcular la desviación típica muestral
Una desviación estándar de una muestra se relaciona con la desviación estándar de una población basada en una muestra aleatoria. Existen una serie de pasos y una fórmula que puedes aplicar para averiguar la desviación típica de una muestra de números.
- Antes de calcular la desviación típica tienes que calcular la media que se identifica con una X con una raya encima.
- Una vez has calculado la media puedes aplicar la fórmula de la desviación típica de un conjunto de números:
Cómo calcular la desviación estándar de una población
La desviación estándar de una población repasa la cantidad de dispersión de los datos de una población entera de los encuestados, es decir que ofrece un parámetro y no una estadística. Hablamos de parámetros cuando se asocia a una propiedad numérica de la población.
En este caso el denominador es igual a n−1 dado que se considera que los valores de la muestra representan una pequeña parte de la población entera. En este caso el denominador n−1 actúa como un factor de corrección para obtener un valor más preciso de la desviación típica.
En los casos donde se conocen todos los valores de la población y no solo una muestra, puede utilizarse la fórmula de la desviación típica poblacional, que es la siguiente:
Calcular la Desviación Estándar usando Excel
Si por el contrario prefieres realizar los cálculos usando directamente una hoja de cálculo puedes aprender a hacerlo desde aquí: Calcular Desviación Típica en Excel